本文共 803 字,大约阅读时间需要 2 分钟。
自动装配:
1、@Autowired的使用
创建MainConfigOfAutowired类
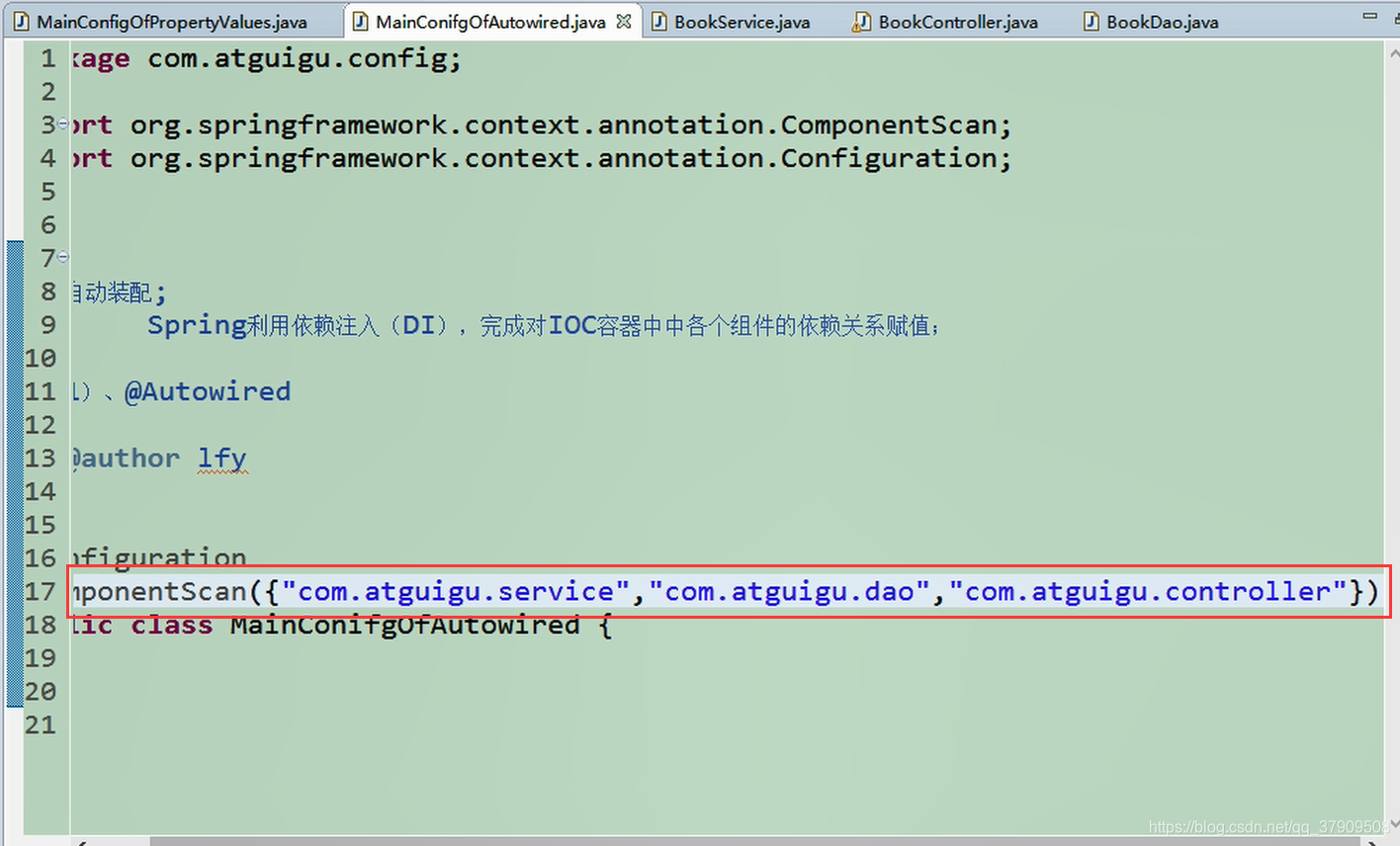
在service层中自动装配
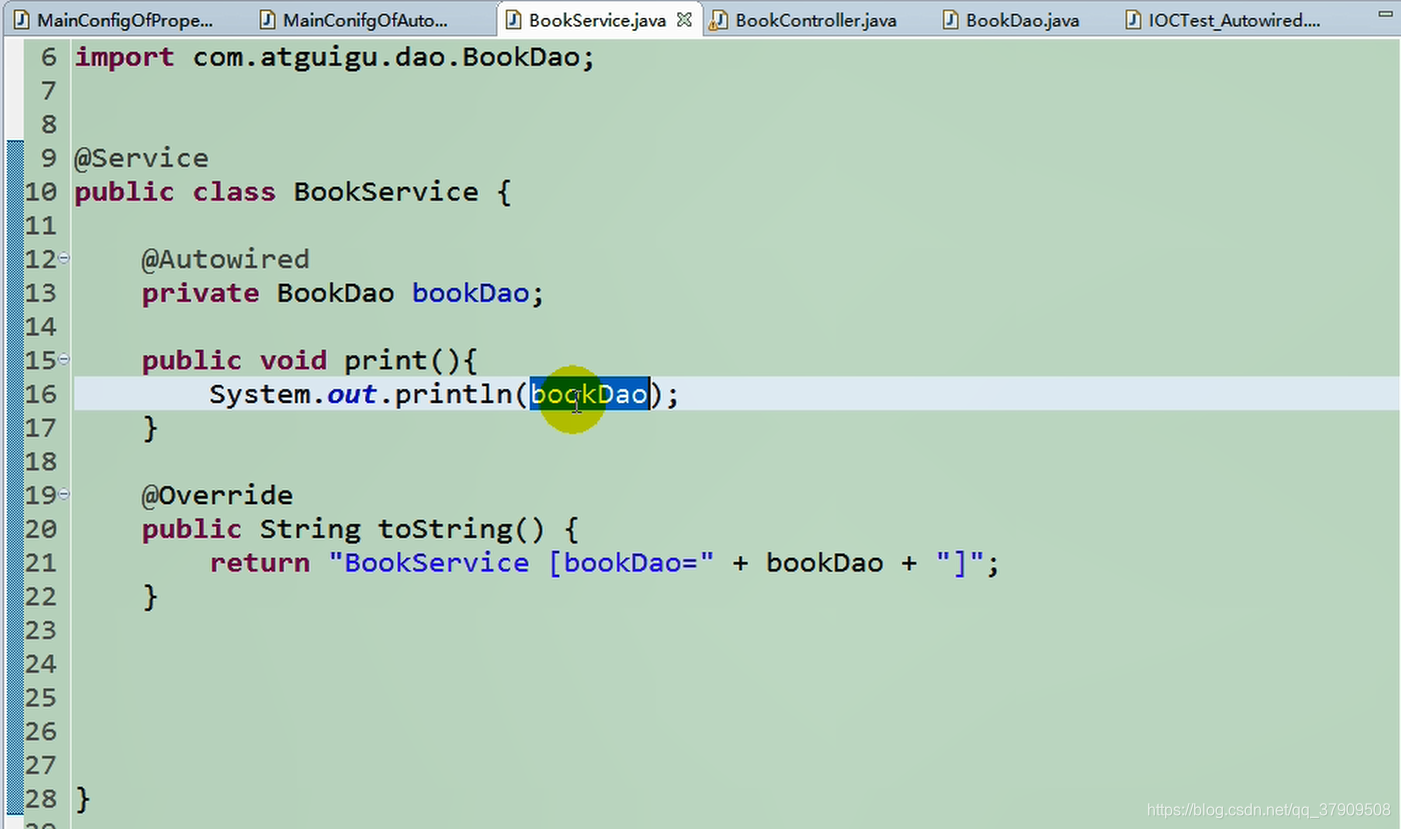
创建IOCTest_Autowired类
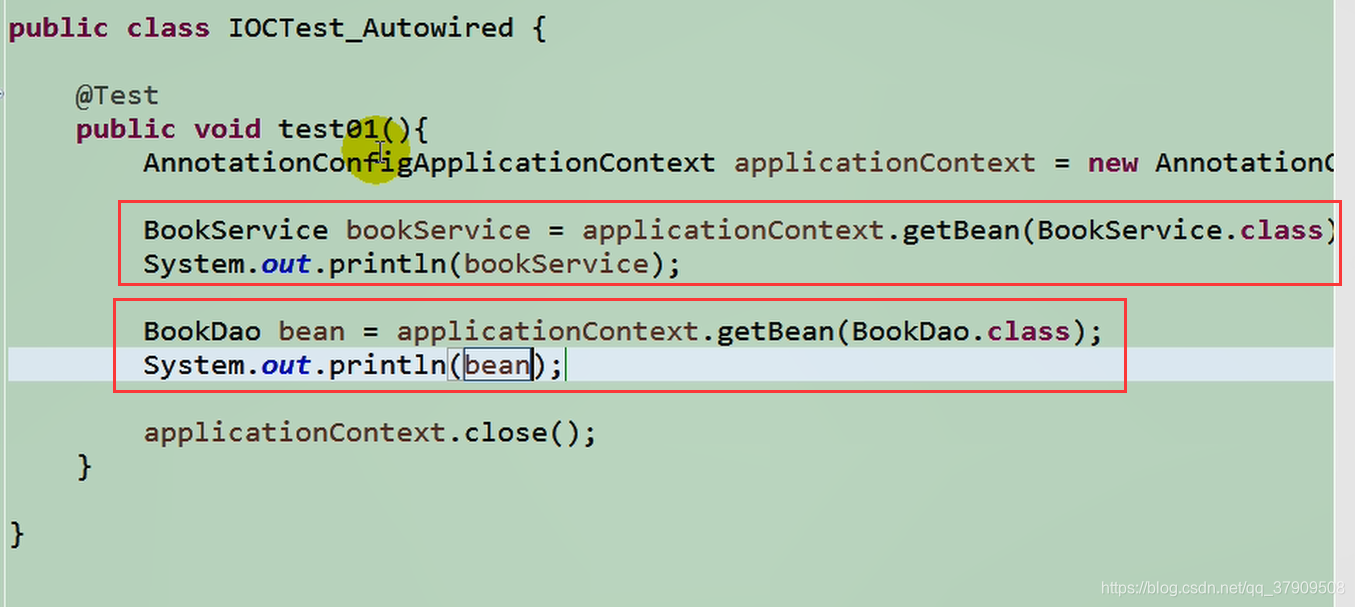
![]()
运行:

对比两个一样的类实现两个bean
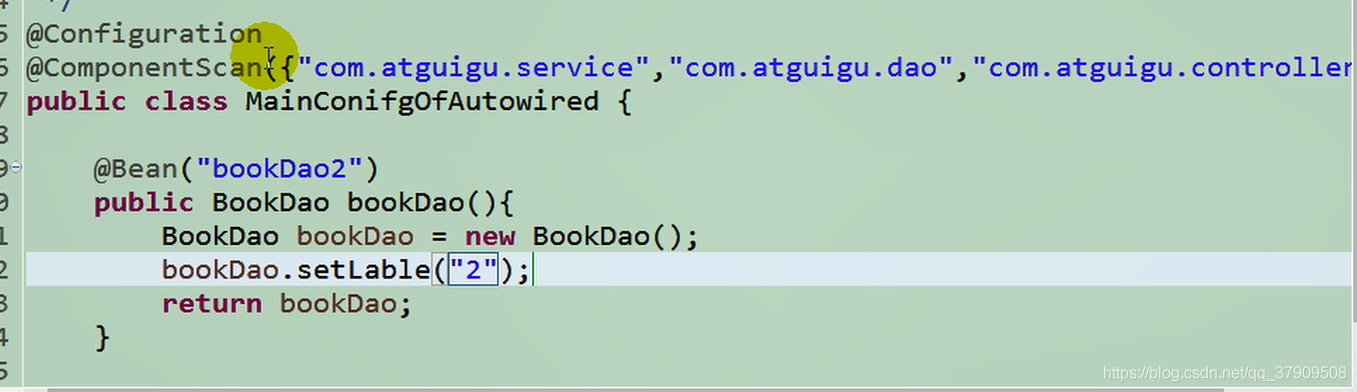
它的bean=“BookDao”

通过注解@Qualifier()指定使用的id名
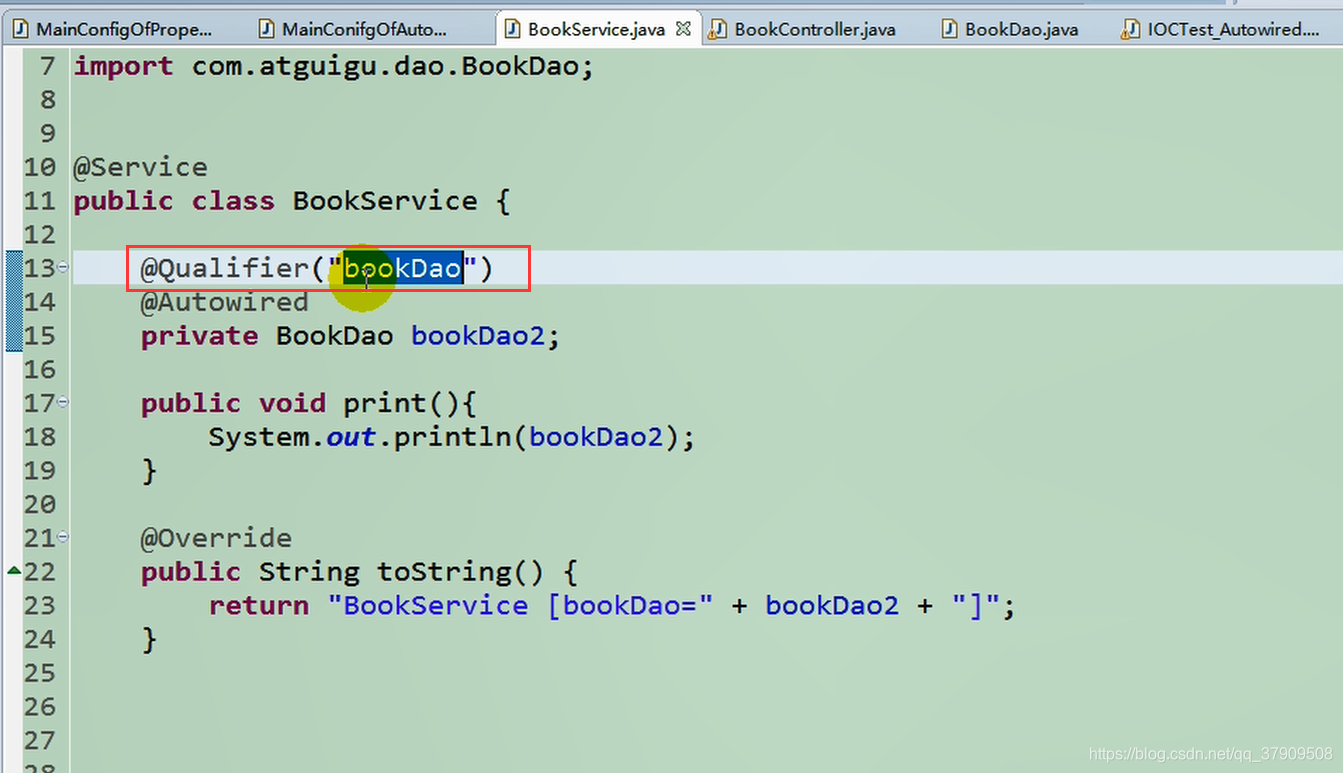
现在删掉相关的bean配置,然后设置required=false,这样不会出现找不到相应的bean而报null异常
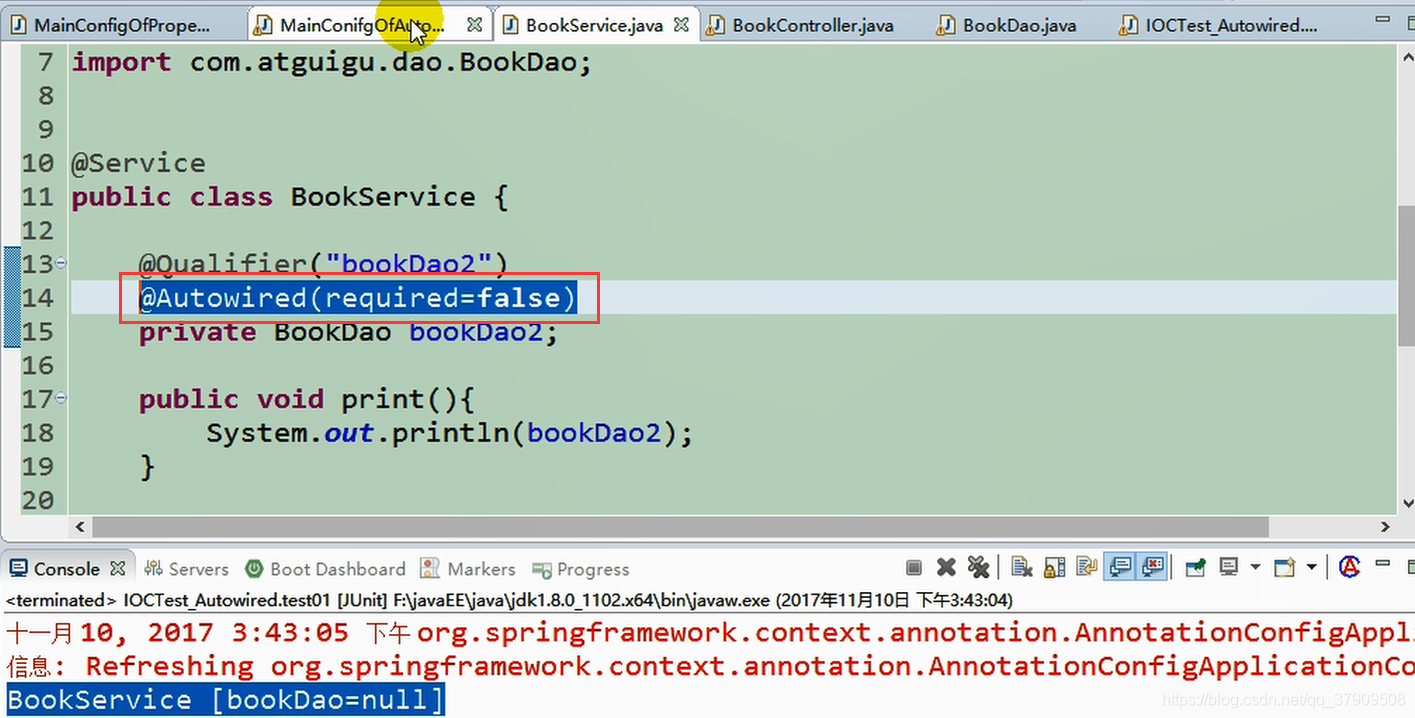
对于@Qualifier()注解还是非常的不方便
使用@Primary,相当于首选项
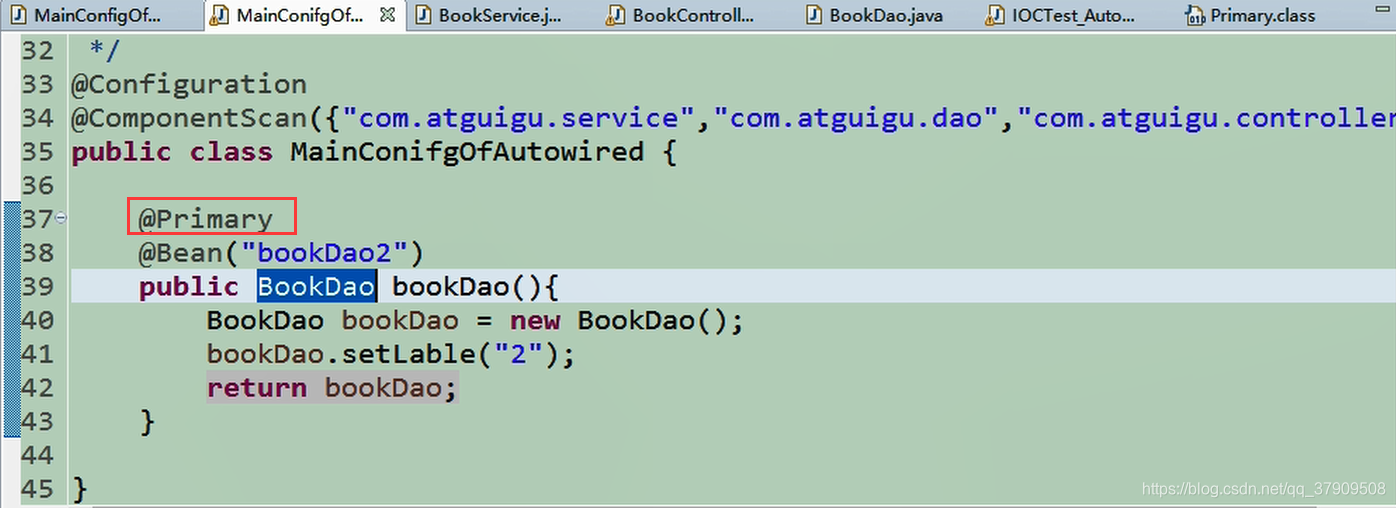
不过在上面的基础上明确指定使用@Qualifier(),那就选择@Qualifier()中的
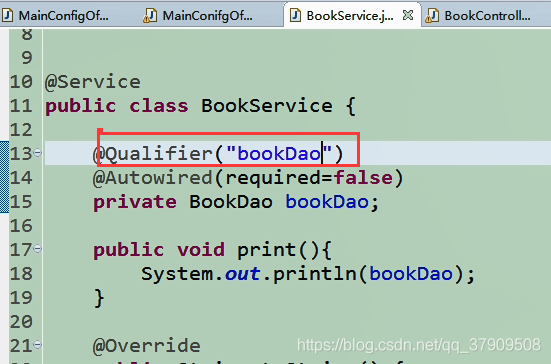
@Autowired不仅可以使用在变量上,还可以使用在方法和构造方法
方法上:
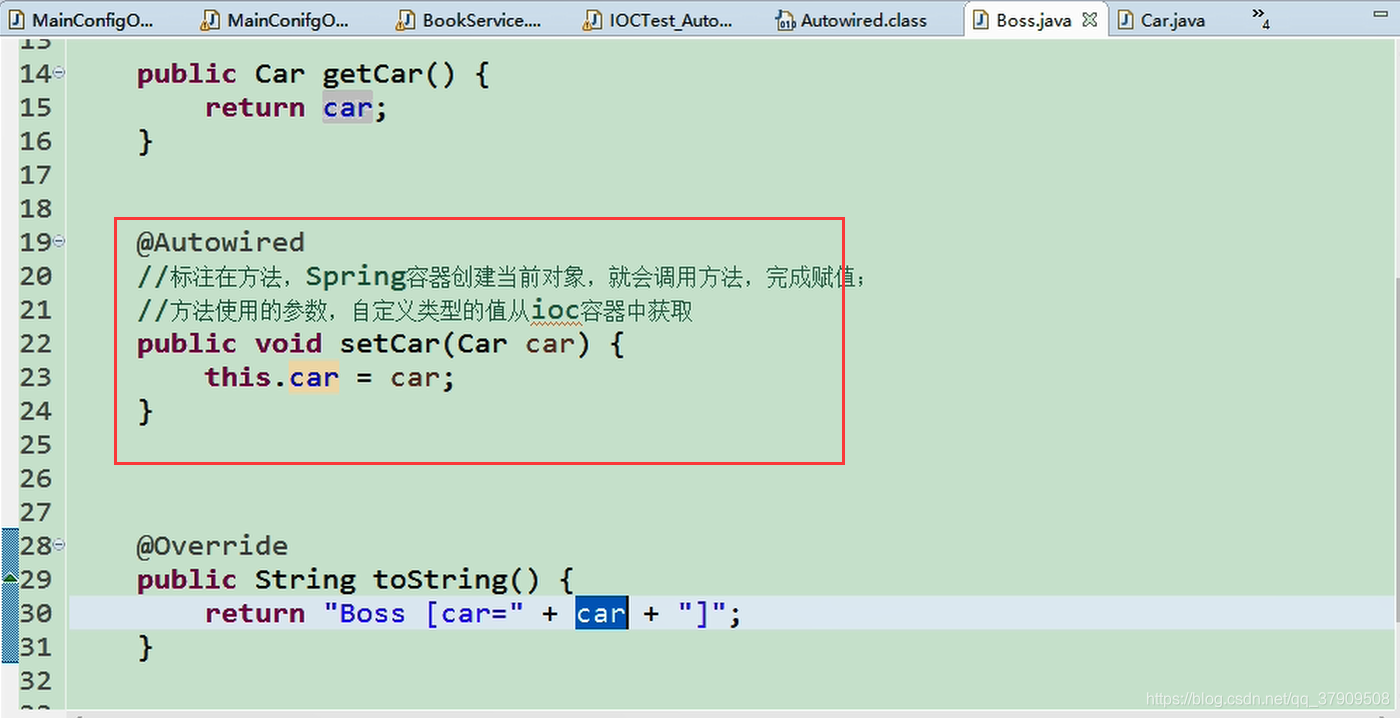
测试函数:
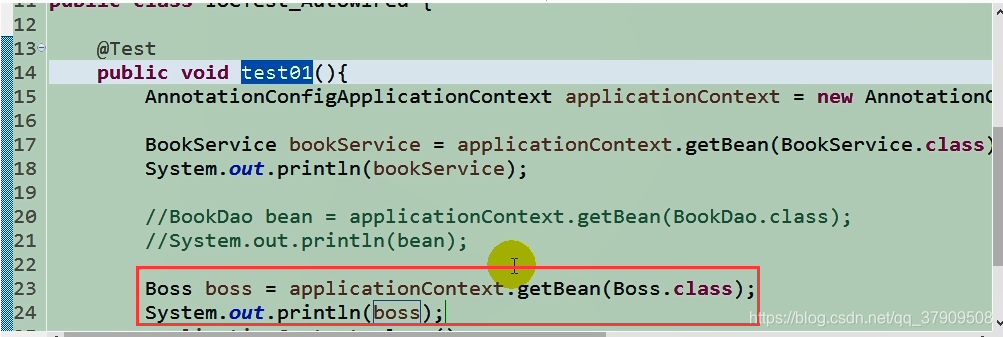
运行:
![]()
同理在构造方法上
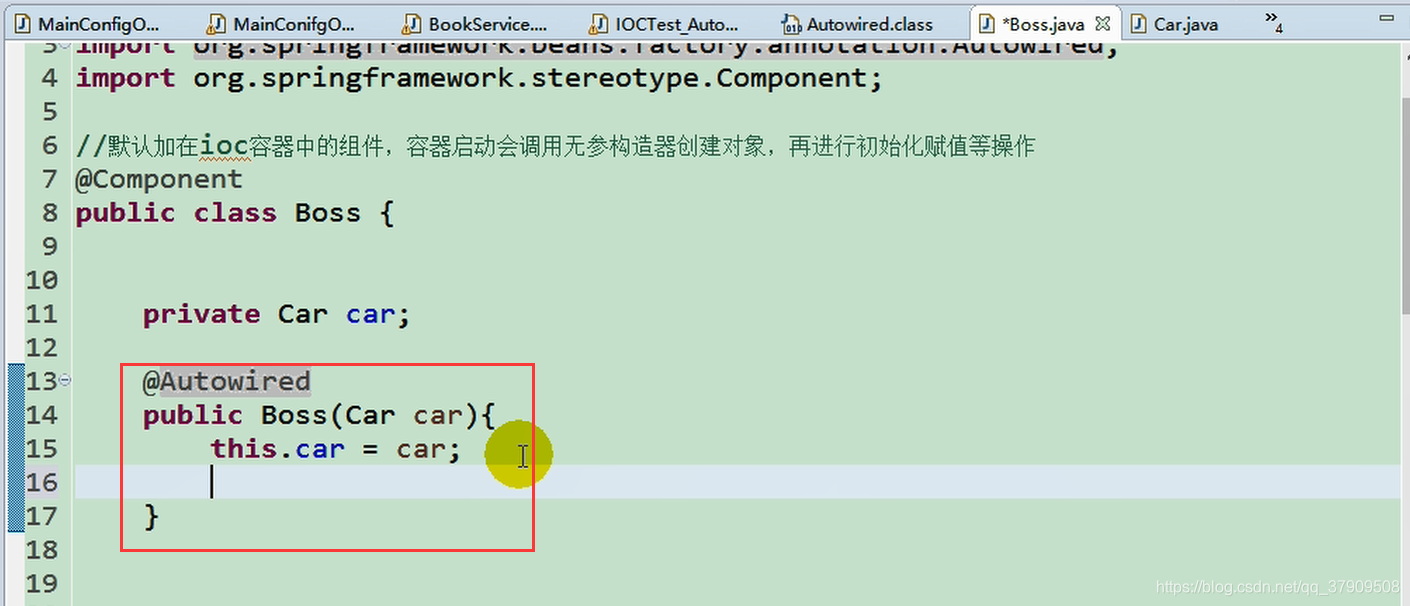
现在我们删掉@Autowired
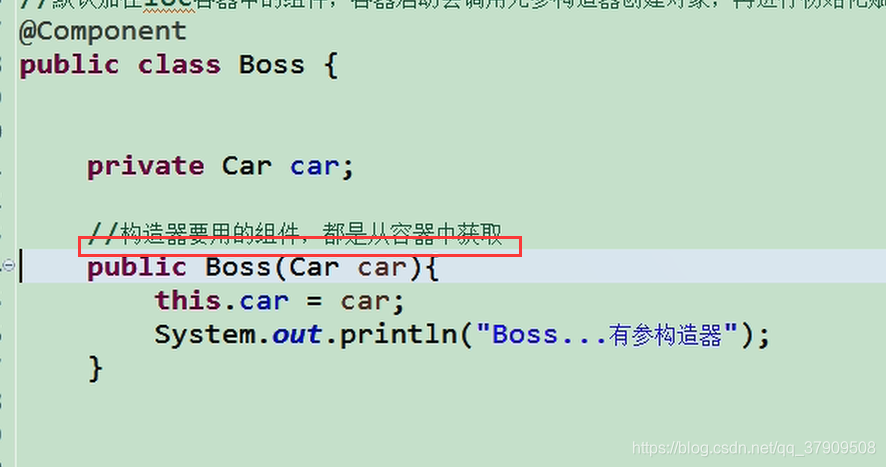
运行
![]()
而且默认从IOC容器中获取
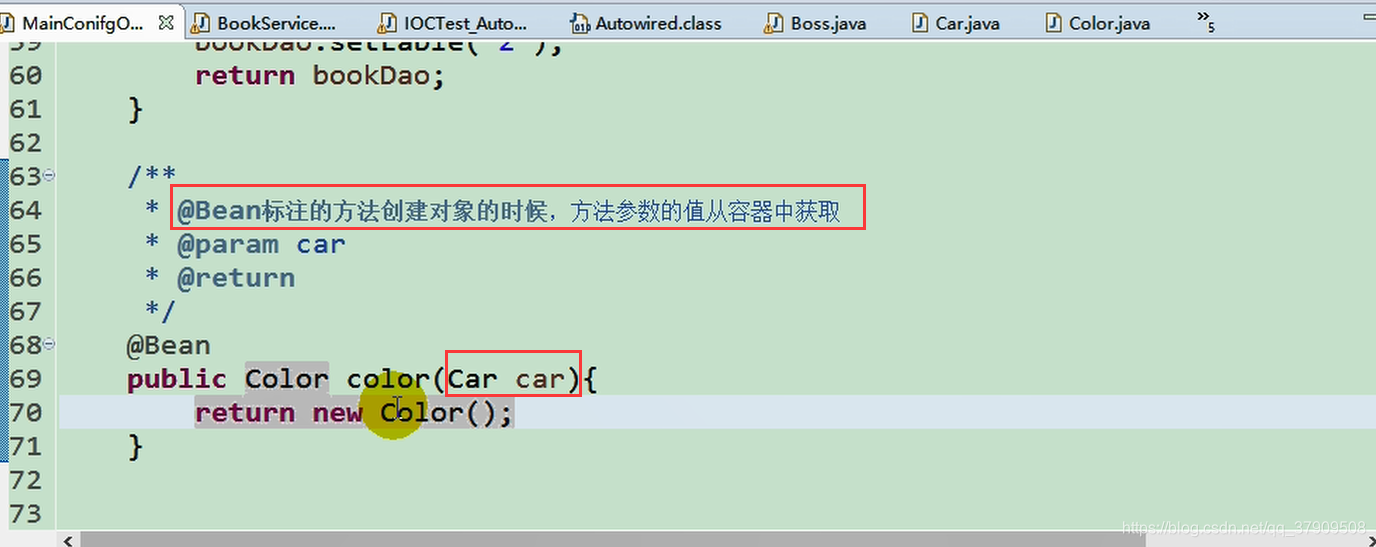
总结:不管 @Autowired放在哪里都会是从IOC容器中获取
2)除@Autowired还可以使用@Resource(JSR250)和@Inject(JSR330):java规范注解
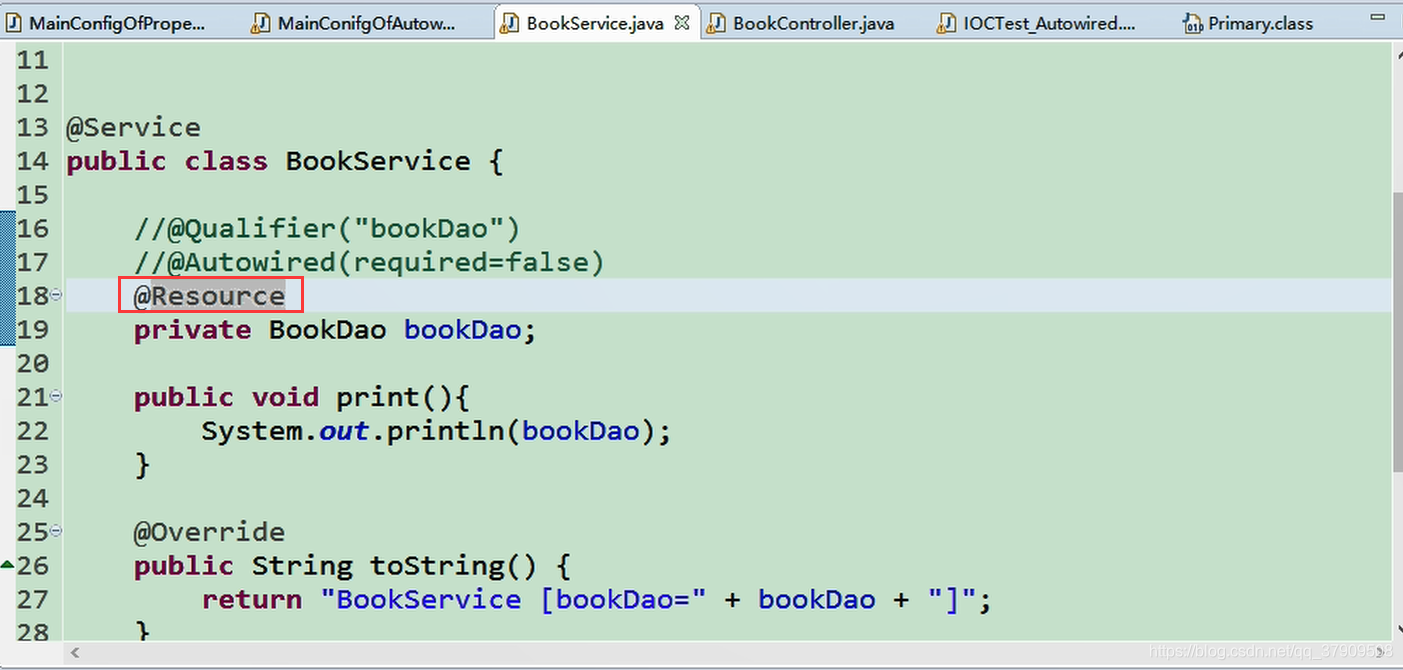
@Resource:功能和@Autowire一样,但是使用的话,其默认id使用的是bookDao(变量名)
但是不能支持@Primary功能、不能支持@Autowired(reqiured=false)
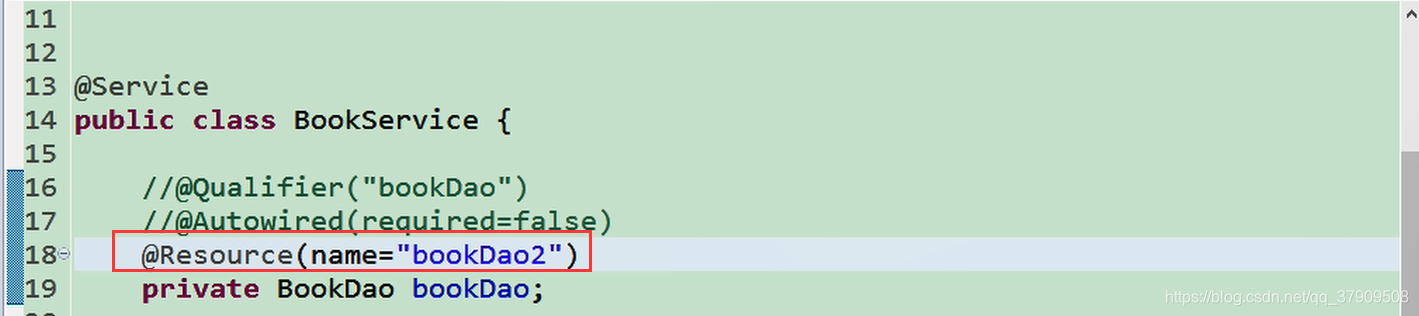
也可以指定
@Inject注解
引入jar包

但是不能支持@Primary功能、不能支持@Autowired(reqiured=false)

将我们自定义一些组件写入到bean,也就是相当于在bean初始化的时候,我们对它的内部在进行一次修改
Aware接口:在实现了该相应接口之后就会在初始化的时候调用相应的方法。
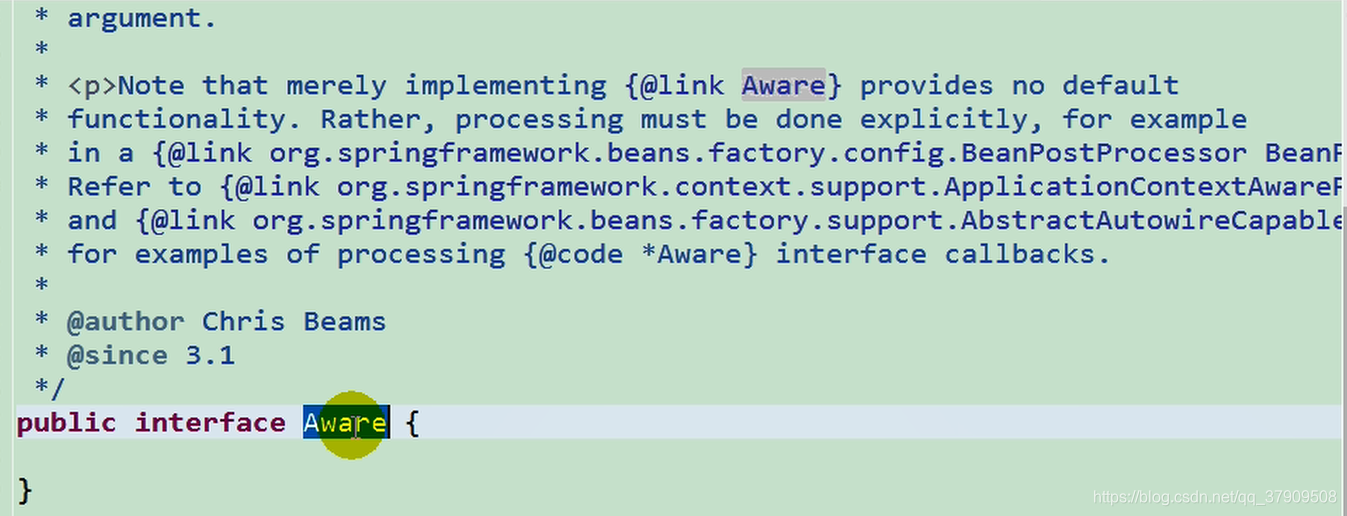
继承它的子类,可以获取IOC的上下文对象
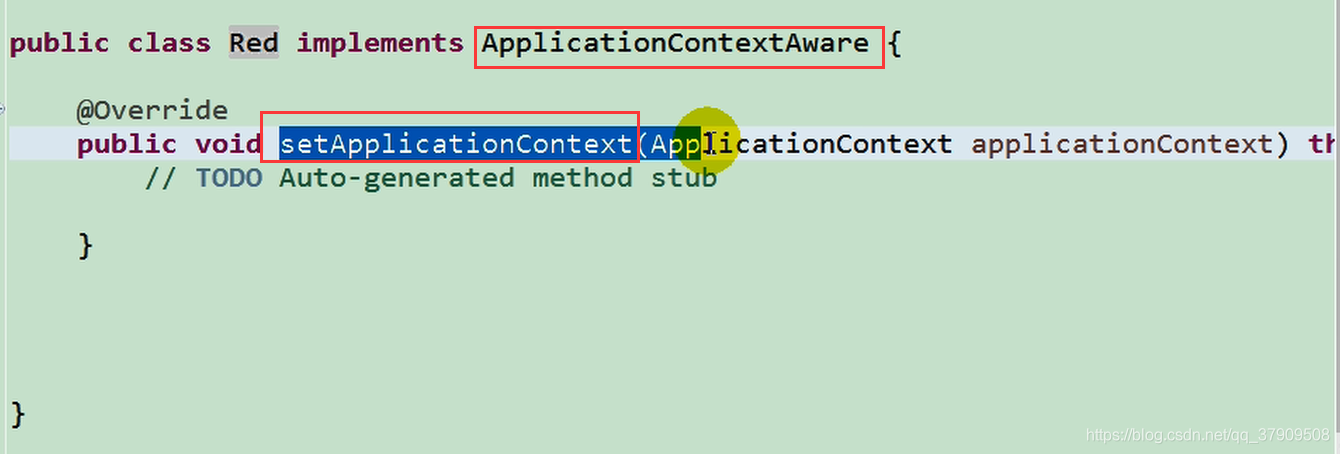
继承子类。获取bean的名字
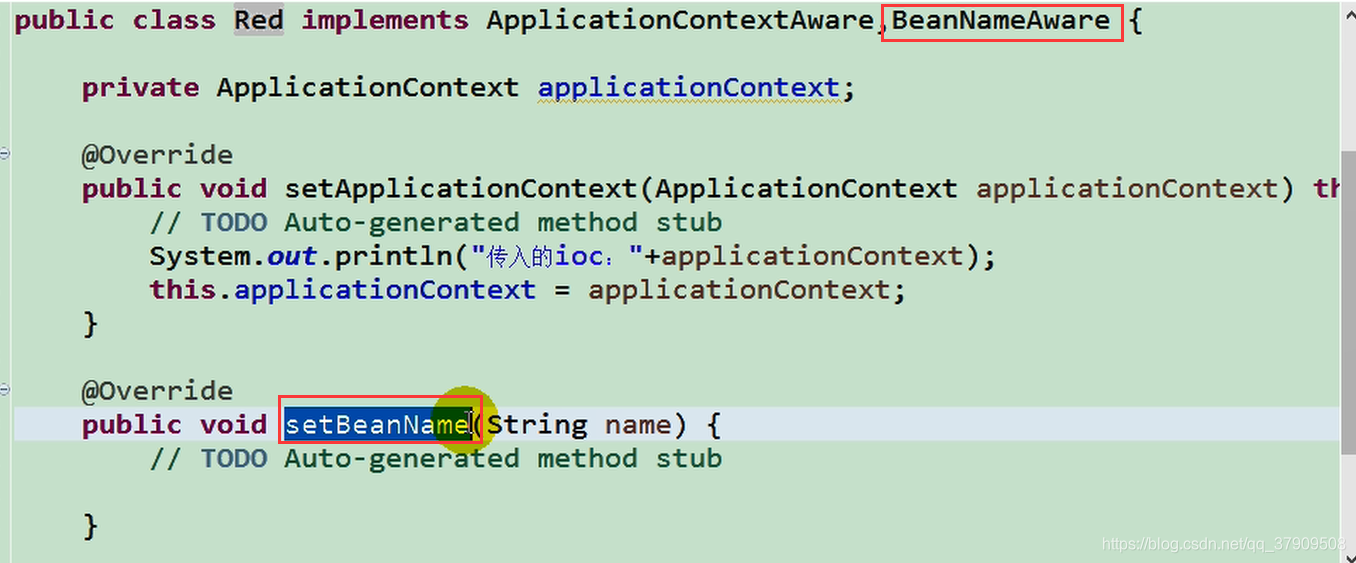
继承子类
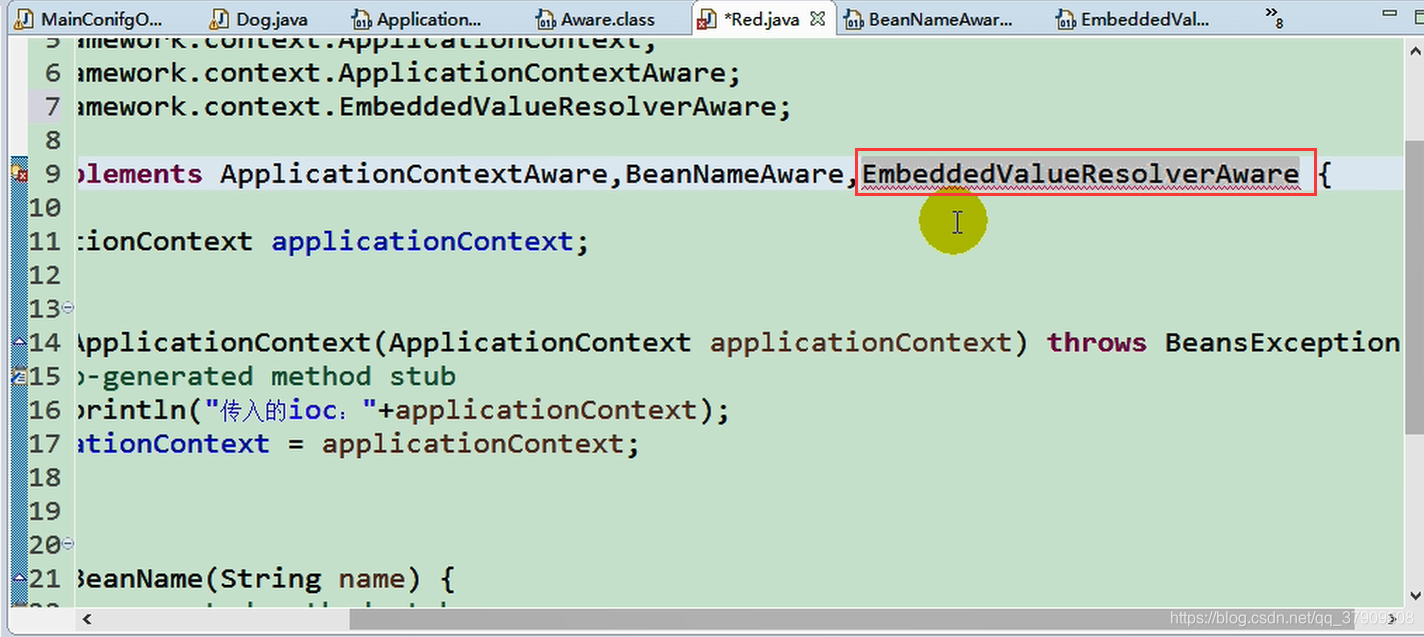
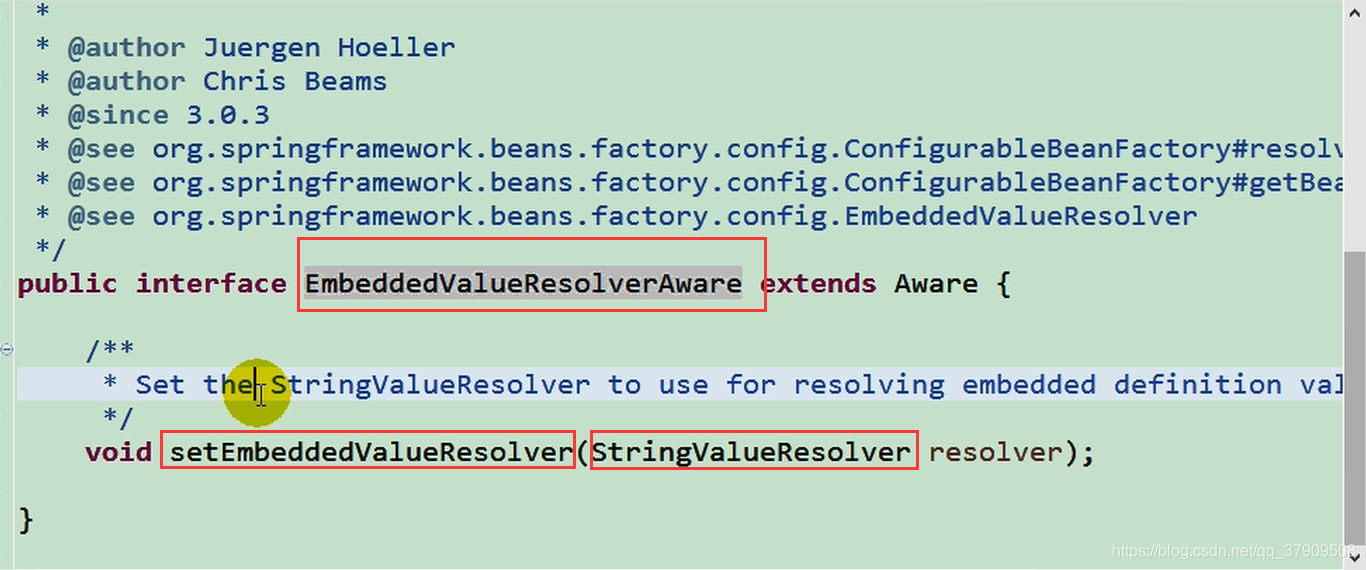

简单来说就是解析占位符和一些特殊表达式的

转载地址:http://jnbhz.baihongyu.com/